La ciencia desde el Macuiltépetl: El chícharo y el sol

Manuel Martínez Morales

Querido Dios: cuando me quede sólo una hora de vida permíteme,

por  favor, pasar ese tiempo en una clase de matemáticas

que me parezca eterna.

Oración de un estudiante aburrido.

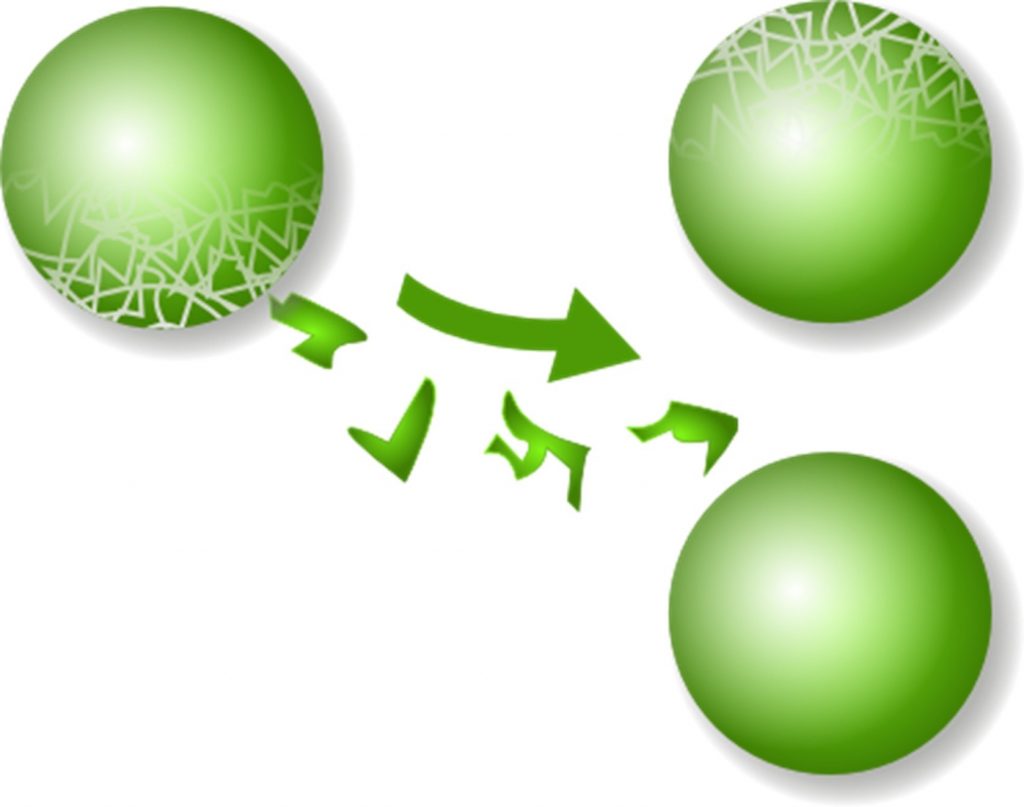
El así llamado Teorema –o Paradoja- de Banach-Tarski, conocido también como el teorema del chícharo y el sol, establece que un sólido de cualquier tamaño, digamos un chícharo, puede descomponerse en un número finito de partes, y luego con estas mismas partes armar otro sólido de cualquier forma y volumen, digamos de la forma y tamaño del sol.

Este teorema matemático, desde su publicación en 1924, causó gran controversia en el ámbito de las matemáticas teóricas e incluso en otros sectores en los que la paradoja fue conocida, al grado de que un ciudadano demandó ante el congreso en el estado de Illinois declarar el postulado fuera de la ley y por tanto la prohibición de su enseñanza en las escuelas. Pues –decían quienes esto proponían- no es posible que se pueda cortar una manzana en cinco piezas y luego reacomodarlas para formar dos manzanas, como si se pudiese crear algo de la nada.

Pero el teorema es válido y aceptado por la comunidad matemática; es decir, el resultado no conduce a contradicciones y la aparente paradoja surge cuando se intenta interpretar el teorema en términos de la realidad física, pues parece contradecir el sentido común: ¿Cómo es posible armar un sólido del tamaño del sol, a partir de los pedazos obtenidos al rebanar un chícharo?

Pero el sentido común muchas veces es ajeno a la rigurosidad de la lógica. Por muchos años los matemáticos revisaron acuciosamente todo el andamiaje que sostenía la demostración del teorema, concluyendo que la aparente paradoja provenía de considerar –en las premisas del teorema- la existencia de ciertos conjuntos “no medibles” y el uso de un controvertido axioma de la teoría de los conjuntos, conocido como el “axioma de elección”.

Aún con esto, el Teorema de Banach-Tarski es impecable desde el punto de vista de la lógica y la matemática. El resultado fue así llamado en honor al matemático Stephan Banach y al lógico Alfred Tarski, quienes lo demostraron –cada uno por su lado- y luego hicieron un trabajo conjunto en el cual dieron la forma definitiva al  teorema.

No ha faltado quien haya intentado crear una “máquina de Banach-Tarski” para duplicar lingotes de oro, ni quien haya intentado relacionar el teorema con el origen del universo. Según esto, el universo conocido fue creado a partir de una gran explosión (el Big Bang), en la cual prácticamente a partir de “nada”  -una singularidad, dicen los físicos- la materia va desenvolviéndose y evolucionando hasta formar el universo tal como lo conocemos.

Si, usted amable lector, está interesado en incursionar en temas científicos tan fascinantes –entretenidos o aburridos, según se miren- le recomiendo la lectura del excelente libro “El chícharo y el sol”, publicado por la Universidad Veracruzana. En este texto el lector asistirá al despliegue de la paradoja Banach-Tarski en un estilo ágil y llano que al mismo tiempo mantiene el rigor que exige la demostración en la metodología matemática.

“El chícharo y el sol” confirma que una teoría matemática no debe considerarse completa hasta que no se aclare tanto que pueda explicarse al hombre de la calle.

Reflexionar para comprender lo que se ve y lo que no se ve.