La ciencia desde el Macuiltépetl: La Conjetura de Goldbach y ajedrecistas bohemios

Manuel Martínez Morales

Con el propósito de hacer más entretenida la hora de la botana y acercar los placeres intelectuales a sus compañeros bohemios, un buen día el profesor Malacates decidió llevar un tablero de ajedrez  a la ilustre cantina Las Glorias de Poncho el Sabio. Por supuesto que tuvo que esperar hasta la tercera ronda de tragos para convencer a sus amigos  que le permitieran enseñarles las reglas básicas del juego.

-Estimados amigos, este noble y apasionante juego no solamente nos brindará entretenimiento durante estas horas de esparcimiento, sino que siendo un ejercicio que reclama mucho más razonamiento que el dominó les ofrece la oportunidad de mantener sus neuronas en buenas condiciones sobre todo a tí, Sidonio, pues sospecho que el Alzheimer te anda rondando ya que van dos o tres veces que olvidas pagar tu cuenta.

-¡Yo le entro!- exclama Chon Tepochas, siempre y cuando apostemos la cuenta del consumo por partido.

-Lo que yo no entiendo profe- dice Sidonio, es cómo está eso de que este jueguito ayuda a fortalecer las neuronas.

-Mira, estimado amigo- responde Malacates, está demostrado científicamente que si a tu edad mantienes activa tu mente, aunque sea resolviendo crucigramas, disminuye la probabilidad de que te ataque el Alzheimer y disminuya tu lucidez mental. Y el ajedrez es un juego que posibilita el desarrollo de tus facultades analíticas, lo que a su vez demanda de una mayor actividad neuronal. Es como una gimnasia mental, y además es divertido una vez que le hayas el chiste.

-A propósito, interviene Mané, también el ocuparse de algún problemilla matemático produce el mismo efecto y también es entretenido. Por ejemplo, en mis días de estudiante universitario mis compañeros y yo nos topamos con uno de estos problemillas, conocido como “la conjetura de Goldbach”. Su enunciado es sencillo y creo que hasta el Chon, que solamente cursó la secundaria, puede entenderlo.

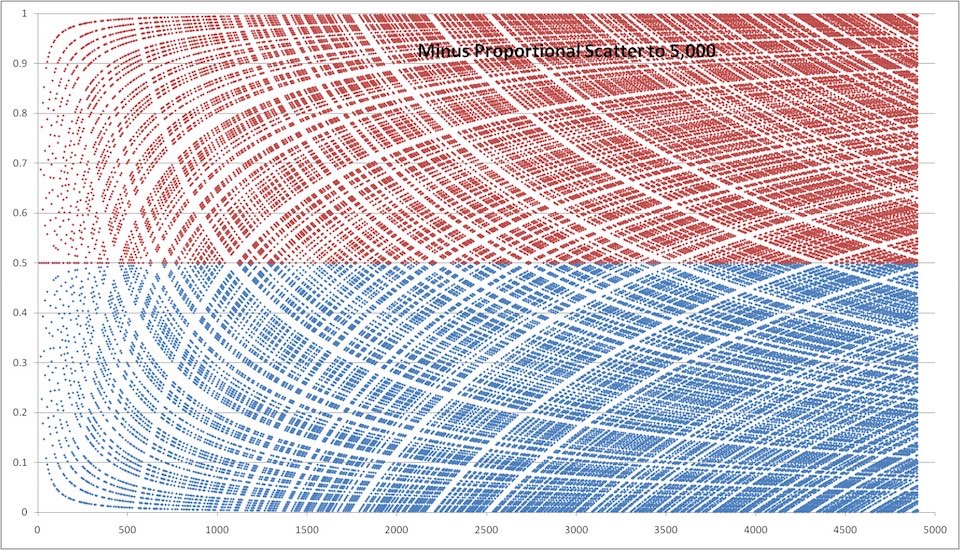
La conjetura, que es una hipótesis cuya verdad no ha sido demostrada ni refutada, propone que todo número entero par, mayor que dos, puede expresarse como la suma de dos números primos.

-¡Pa sú!, ¿qué acaso hay números primos, sobrinos y hermanos?

-No se confundan, replica Mané, se llama número primo a aquel que sólo puede descomponerse como el producto de él mismo por 1. Por ejemplo el número 12  puede expresarse como 12=6×2, o como 12=2x2x3; por lo que no es un número primo. En cambio, el número 7 solamente puede descomponerse como 7=7×1, o el 19=19×1, y no tienen más factores. Por tanto el 7 y el 19 son números primos.

Y la conjetura mencionada afirma que todo número par, mayor que 2, puede expresarse como la suma de dos números primos, por ejemplo 12=7+5; 20=17+3, etcétera. El asunto es que hasta el momento no se ha encontrado ninguna excepción al enunciado, que con el uso de computadoras ha sido probado para números muy grandes, lo que bastaría para refutar la conjetura, pero tampoco ha sido posible demostrarla matemáticamente para todos los pares que forman un conjunto infinito, lo cual convertiría la conjetura en un teorema.

-Pues  si hasta yo  entendí, comenta  Chon, quiere decir que no debe ser muy difícil demostrarla pues trata con puros números enteros positivos, que ya en la primaria y secundaria se estudian bastante bien.

Sin embargo, resulta que el asunto no es tan sencillo pues desde su enunciado, en 1742, por el matemático Christian Goldbach, este problema ha desafiado las mejores mentes matemáticas del mundo y hasta la fecha no se ha dado con su solución, aún empleando sofisticados métodos lógicos y matemáticos.

Lo más llamativo es que debido a su aparente simplicidad todo estudiante de ciencias exactas, en algún momento de su formación, ha creído que puede demostrar la conjetura con métodos simples de la teoría de números y ha pasado noches de desvelo intentándolo pues además resulta un ejercicio bastante interesante y entretenido, provocando que el osado novato aprenda más matemáticas de las que podría asimilar en los cursos normales.

Algunos matemáticos con inclinaciones lúdicas y literarias han creído que la solución a la conjetura podría plantearse como un problema combinatorio y que eso la conecta con el ajedrez. O, como plantea el matemático Apóstolos Doxiadis en su conocida novela El tío Petros y la Conjetura de Goldbach, ejercitarse en el ajedrez ayudaría a atacar problemas cómo el encerrado en la conjetura: “El cambio que se produjo en la vida del tío Petros como consecuencia del ajedrez fue notable. Desde el momento en que había decidido dedicarse a probar la conjetura de Golbach, de lo que ya hacía unos diez años, casi no se había dado un momento de descanso o distracción. Sin embargo, para un matemático es absolutamente esencial sustraerse temporalmente de la tarea que tiene entre manos. Para asimilar el trabajo y elaborar sus resultados en un nivel inconsciente, la mente necesita tanto del esfuerzo como del ocio. Del mismo modo que una investigación que tenga por objeto conceptos matemáticos a menudo produce efectos vigorizadores en un intelecto sosegado, también puede volverse intolerable cuando el cerebro sufre la fatiga derivada de un esfuerzo incesante.”

Así que, amigos bohemios, concluye Mané alzando su vaso, cuidemos nuestra salud combinando esfuerzo y ocio, ajedrez y chelas en su debida proporción, y aderecemos la rica botana que aquí se sirve con las eruditas disertaciones del profe Malacates sobre conjeturas matemáticas y otras historias edificantes, como la del tío Petros. ¡Salud!

Reflexionar para comprender lo que se ve y lo que no se ve.