Albert Einstein presenta su Teoría de la Relatividad General, el 25 de noviembre de 1915

El 25 de noviembre de 1915, Albert Einstein presentó la formulación definitiva de su Teoría de la Relatividad General en la Academia Prusiana de Ciencias, introduciendo el misterioso concepto de la curvatura del espacio-tiempo. Esto lo logró tras casi una década de tortuosos intentos de compatibilizar la fuerza gravitatoria con su teoría especial de la relatividad (1905). Ese día por fin dio forma precisa y definitiva a la que se considera una de las cimas intelectuales de la humanidad e hizo la publicación de la misma.

Ese día también presentó su ecuación de la relatividad general, la cual, en realidad es un sistema de diez ecuaciones, pero se pueden escribir de manera unificada, utilizando una sola vez el signo “=”, y resumirlas en una sola: R_μν -1/2 g_μν R = 8πG T_μν. En la forma original en la que la escribió Einstein en su artículo, la notación (por ejemplo usaba índices latinos en lugar de griegos) y la distribución de los términos era ligeramente distinta, pero aún así, es totalmente equivalente a esta.

En lenguaje común, la nueva ecuación de Einstein relaciona dos aspectos: curvatura del espacio-tiempo ↔ Masa (energía). Por ponerlo en contexto, anteriormente la teoría de la gravedad de Newton, el mayor éxito de la revolución científica del siglo XVII, aportaba dos leyes que podemos visualizar así:

Masa → Gravedad; y

Fuerza de gravedad → Movimiento de cuerpos masivos,

donde “→” podemos leerlo como “crea”.

Es decir, una masa –por ejemplo, la Tierra– crea un campo gravitatorio, que a su vez ejerce una fuerza que controla el movimiento de otras masas, como una manzana o la Luna. Con la aportación de Einstein, la teoría de Newton se veía ahora desbancada por otra que la incluía como una aproximación solo válida para masas y velocidades relativamente pequeñas. Pero la teoría de Einstein era mucho más que un refinamiento de la de Newton: cambiaba completamente el concepto de qué es y cómo actúa la gravedad.

Entre la visión clásica del mundo de Newton y la relativista de Einstein, hay dos diferencias esenciales. Por una parte, en la formulación de Einstein desaparece la noción de gravedad, que ha sido sustituida por algo más misterioso y sugerente: la curvatura del espacio-tiempo. Y, por otra, unifica en una sola ecuación las dos leyes básicas de la teoría newtoniana. Es decir, ambas “→” quedan aunadas en una sola “↔”. Sin duda alguna, la eliminación de la gravedad como una fuerza ‘real’ y su interpretación como un ‘efecto aparente’ de la curvatura del espacio-tiempo es el elemento más revolucionario de la teoría. De esta manera, Einstein explicaba con una simplicidad pasmosa la observación de Galileo de que, en ausencia de fricción, todos los cuerpos caen al mismo ritmo: los objetos se mueven en un mismo espacio-tiempo que, al estar curvado, produce la impresión de movimiento bajo una fuerza que actúe sobre ellos.

¿Podemos visualizar el concepto de la curvatura del espacio-tiempo?

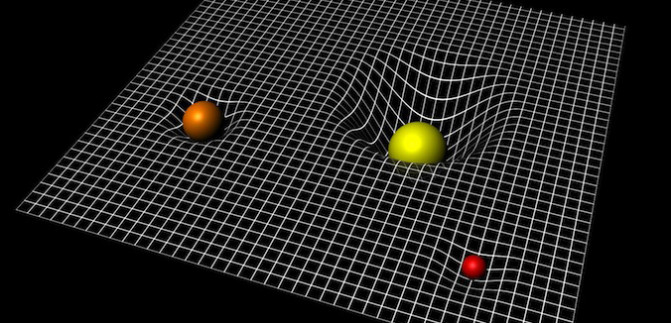
Es habitual representar los efectos la curvatura del espacio tiempo, como el movimiento de canicas en una cama elástica deformada por el peso de una masa mayor. Aunque ilustrativa, esta analogía no consigue transmitir el hecho esencial de que la curvatura del espacio-tiempo apenas afecta las direcciones espaciales de la cama elástica, sino que se produce mayoritariamente en la dirección del tiempo. La teoría es demasiado rica y sutil como para dejarse capturar completamente por analogías e imágenes simplificadas.

La representación de la curvatura del espacio-tiempo como una ‘cama elástica’ presenta limitaciones. / ESA–C.Carreau

Pero no hay forma de representar de manera sencila esto, si no que para darle una dimensión completa habría que utilizar distintas imágenes para ilustrar diferentes aspectos de la teoría, pero no hay una que lo capture todo correctamente. Lo de la cama elástica está bien, pero tiene limitaciones serias. Por ejemplo, no sirve para ilustrar ni medianamente bien lo que es un agujero negro, y da lugar a confusiones: ¿Cómo es que decimos que la curvatura es tan pequeña que no la notamos habitualmente y, sin embargo, es suficientemente grande como para que un proyectil, o la Luna, sigan una trayectoria curva en lugar de recta? Habría que explayarse mucho para explicar que nos movemos mucho más en el tiempo que en el espacio, y lo que eso conlleva.