Manuel Martínez Morales
Desde muy joven tuve que trabajar para poder continuar mis estudios universitarios y más tarde los estudios de posgrado. Debo decir que ha sido por pura casualidad que he aprendido muchas cosas de lo poco que conozco. Así fue como en una temporada tuve la oportunidad de trabajar en lo que entonces se conocía como programador y analista, trabajo consistente en escribir programas de cómputo con propósitos específicos, en el Colegio de México. En algún momento desarrollé programas para un par de distinguidos economistas que ahí laboraban cuyos nombres por ahora no recuerdo. Actividad por demás interesante ya que estos investigadores no sólo nos daban las fórmulas y datos para calcular los indicadores que les interesaban, sino que además nos explicaban detalles del significado de tales índices y sus propiedades, lo cual no solamente nos ilustraba sino que nos daba elementos para realizar mejor nuestro trabajo. Por ejemplo si nos pedían calcular el índice de Gini, que sirve para medir la desigualdad de ingresos en alguna región, nos explicaban cómo se interpretaba éste e indicaban que tomaba valores entre 0 y 1.
De modo que si al hacer el cálculo de este indicador obteníamos un valor, por ejemplo, de 4.65 inmediatamente nos percatábamos que debía haber un error en el programa o los datos. Es decir, esa información adicional que nos proporcionaban quienes solicitaban los programas nos permitía, en su caso, hacer las correcciones apropiadas y entregar resultados consistentes.
Y resulta que con el paso de los años soy un convencido que la matemática aplicada nos permite comprender mejor la realidad –ya sea en el nivel físico, biológico o social- pues nos proporciona una “radiografía” de los fenómenos estudiados permitiendo -si hacemos una interpretación adecuada en el contexto del marco teórico y metodológico que estemos empleando- ver más allá de lo aparente, esto es pasar del fenómeno al concepto.
También he aprendido que para iniciar una investigación, o simplemente comprender algún aspecto de la realidad en que estamos inmersos, hay muchas puertas de entrada.
En los tiempos actuales, en el aquí y ahora de México y su inserción en eso que eufemísticamente se llama globalidad es necesario, si está a nuestro alcance hacerlo, usar las matemáticas para calar en la realidad, esta realidad que en momentos resulta lacerante para un gran número de mexicanos.
Así pues, al percatarnos que vivimos en una sociedad injusta, desigual, con la mayoría debatiéndose en la pobreza, y con un gobierno autoritario y despiadado, hay que hacer un esfuerzo por comprender “la razón profunda de las cosas” –según aconsejaba Augusto César Sandino- y estar en condiciones de actuar para transformar esta realidad y avanzar hacia una convivencia social igualitaria.
Cuando hace más de un siglo y medio, Carlos Marx trató de comprender esta situación en el seno de una sociedad envuelta por el modo de producción capitalista, entró directamente al análisis en el terreno de la producción económica, proponiendo como eje de su análisis el concepto de mercancía, que a su vez reflejaba la diferencia entre valor de uso y valor de cambio de los productos, conceptos que sustentaban su análisis para explicar las contradicciones fundamentales de ese tipo de economía, explicando el por qué de las disparidades entre salario y capital y las contradicciones a que esto conducía, entre otras las profundas desigualdades sociales consustanciales al capitalismo y que persisten hasta nuestros días en forma aguda.
Por otra parte, Thomas Piketty, en El capital en el siglo XXI, aborda un estudio similar pero ahora partiendo directamente del análisis de la desigualdad en los ingresos por trabajo y los del capital la cual, sostiene, siempre ha constituido la primera dimensión del conflicto distributivo, es decir de la desigualdad social en sus diversas formas.
Para quienes no somos especialistas en economía, la matemática nos puede ayudar a comprender el fenómeno de la desigualdad, para lo cual podemos empezar por considerar el coeficiente de Gini, que es una medida de la desigualdad normalmente utilizada para medir la desigualdad de los ingresos, dentro de un país, pero puede utilizarse para medir cualquier forma de distribución desigual.
El coeficiente de Gini es un número entre 0 y 1, en donde 0 se corresponde con la perfecta igualdad (todos tienen los mismos ingresos) y donde el valor 1 se corresponde con la perfecta desigualdad (una persona tiene todos los ingresos y los demás ninguno).
El índice de Gini es el coeficiente de Gini expresado en porcentaje y es igual al coeficiente de Gini multiplicado por 100.
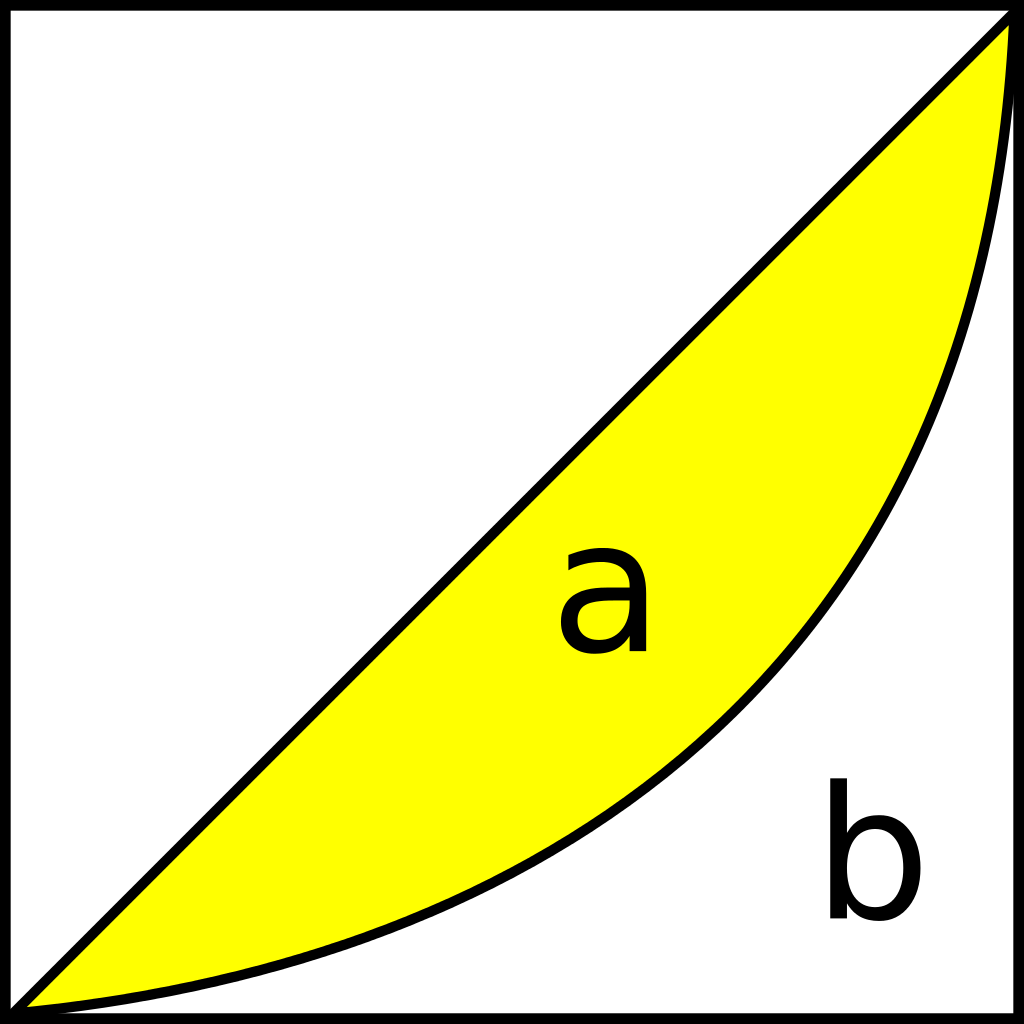
Para quienes tienen curiosidad matemática, apuntaremos que el coeficiente de Gini se calcula como una proporción de las áreas en el diagrama de la curva de Lorenz. Si el área entre la línea de perfecta igualdad y la curva de Lorenz es a, y el área por debajo de la curva de Lorenz es b, entonces el coeficiente de Gini es a/(a+b). De forma resumida, la curva de Lorenz es una gráfica de concentración acumulada de la distribución de la riqueza superpuesta a la curva de la distribución de frecuencias de los individuos que la poseen, y su expresión en porcentajes es el índice de Gini. (Ver figura anexa)
Esta proporción se expresa como porcentaje o como equivalente numérico de ese porcentaje, que es siempre un número entre 0 y 1. El coeficiente de Gini se calcula a menudo con la fórmula de Brown, que es más práctica y que no mostraremos aquí.
Para ejemplificar su empleo e interpretación, que es lo que interesa, veamos el índice de Gini para algunos países, comparados con México (recuerde que mientras más cercano a 1, el índice refleja mayor desigualdad; si es más próximo a 0, representa menor desigualdad), con cifras del año 2012:
Honduras, 0.60
Guatemala, 0.52
Chile, 0.51
México, 0.48
Argentina, 0.42
Estados Unidos, 0.41
Alemania, 0.31
Dinamarca, 0.29
Finlandia, 0.27
De estas cifras puede verse que existe mayor desigualdad en el ingreso que en México, en Honduras, Guatemala y Chile; en tanto que en Argentina, Estados Unidos, Alemania, Dinamarca y Finlandia hay una mayor igualdad en la distribución del ingreso que en nuestro país. (La tabla completa para todos los países puede consultarse en: http://datos.bancomundial.org/indicador/SI.POV.GINI )
En tanto que por entidad federativa se tiene:
Oaxaca, 0.49
Chiapas, 0.47
Veracruz, 0.45
Aguascalientes, 0.44
Baja California, 0.43
Distrito Federal, 0.41
Tomando en cuenta que el índice de Gini promedio nacional es de 0.48, puede observarse que Veracruz está por debajo de esa media, superándolo en desigualdad, por ejemplo, los estados de Chiapas y Oaxaca. En tanto, en los estados de Aguascalientes, Baja California y el Distrito Federal existe menor desigualdad en la distribución del ingreso que en Veracruz. (La tabla completa con todos los estados puede consultarse en: www3.inegi.org.mx/Sistemas/…/LeerArchivo.aspx?ct=41229&c)
En breve, el coeficiente de Gini es una especie de radiografía de la realidad económica y social. De alguna manera condensa la condición de desigualdad en una región, y proporciona elementos explicativos de por qué esta desigualdad en los ingresos se asocia con los otros tipos de desigualdad, que también se pueden cuantificar con variantes de este coeficiente.
Entonces, ciertos indicadores numéricos interpretados adecuadamente pueden ser una puerta de entrada para el análisis de lo que ocurre en nuestra sociedad. Para lo cual es aconsejable contar con una cultura matemática básica, que permita al ciudadano al menos entender el sentido de estadísticas e indicadores como el coeficiente de Gini y sea capaz de interpretarlos sin que necesariamente conozca la forma de calcularlos. Los educadores tienen la palabra.