La ciencia desde el Macuiltépetl: Sobre imágenes y matemáticas

Manuel Martínez Morales

El pensamiento abstracto está siempre ligado, en una forma u otra, a imágenes concretas. Si se medita detenidamente en esta conexión, se encuentran cosas sorprendentes. Por ejemplo, la invención de la geometría analítica atribuida a René Descartes, consiste fundamentalmente en asociar figuras geométricas con ecuaciones matemáticas, lo cual a mi juicio consistió en una verdadera revolución científica. Cuando estudié por primera vez la materia, en preparatoria, me llevó un buen tiempo comprender cabalmente esta relación entre figuras geométricas y ecuaciones.

Con el paso del tiempo, tanto en matemáticas como en lógica y en varias de las ciencias fácticas, se han desarrollado conceptos, métodos y técnicas para construir imágenes a partir de relaciones numéricas o lógica. Tanto así que existen diversas modalidades de lo que se dado en llamar mapas conceptuales.

En mi propio quehacer en el campo de la inteligencia artificial he empleado y diseñado varias metodologías para representar gráficamente conocimiento y/o relaciones lógicas entre conceptos. En esta disciplina existen áreas como el análisis formal de conceptos, la geometría de conceptos y otras más que son de gran utilidad, tanto teórica como práctica. En su mayor parte, consisten en establecer una relación entre figuras geométricas y relaciones lógico conceptuales, dando lugar a lo que algunos llaman espacios conceptuales, pues la relación entre grafos y conceptos puede ubicarse en un espacio geométrico que incluso puede contener una métrica, es decir una medida de distancia entre conceptos o que auxilie en su clasificación o en la derivación de nuevos conceptos.

Recientemente se ha dado a conocer una nueva familia de este tipo de representaciones gráficas asociadas a una estructura matemática, conocida como diagramas de Voronoi. Clara Grima, profesora de la Universidad de Sevilla expresa que el diagrama de Voronoi (que debe su nombre al matemático ruso Georgy Voronoi) es una estructura tan sencilla e intuitiva que hasta un niño de tres años puede entenderla.

El diagrama de Voronoi de un conjunto de puntos en el plano es la división de dicho plano en regiones, de tal forma, que a cada punto le asigna una región del plano formada por los puntos que son más cercanos a él que a ninguno de los otros objetos. Dicho de otra manera, lo que hace dicho diagrama es dividir el plano en tantas regiones como puntos u tengamos de tal forma que a cada punto le asignemos la región formada por todo lo que está más cerca de él que de ningún otro.

Piensen por ejemplo, continúa Grima,  en el plano de una ciudad y dibujen sobre él un punto por cada una de las farmacias que hay en la misma. En el caso más simple, si solo hubiese una farmacia en la ciudad la región de Voronoi de dicha farmacia sería toda la ciudad, porque todos están más cerca de dicha farmacia que de ninguna otra, puesto que no hay más. Fácil, ¿verdad?

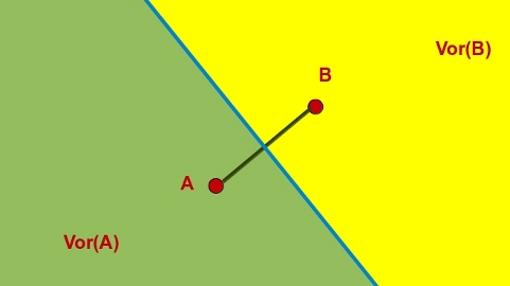Si hubiese dos farmacias, A y B, la ciudad quedaría dividida en dos, los que están más cerca de la farmacia A que de la farmacia B (llamaremos a esta zona Vor(A)) y los que son más cercanos a la B que la A (a esta la llamamos Vor(B)). Bueno, y los que están a la misma distancia de los 2. En honor a Euclides y aquello de que el camino más corto entre dos puntos es la línea recta, mediremos la distancia en la ciudad como la longitud del segmento que une a dos puntos. Así, los puntos que están a la misma distancia de ambas farmacias son los que están sobre una recta: la mediatriz entre los dos puntos que definen las farmacias en el plano y que no es más que la recta perpendicular al segmento que une A y B por el punto medio de este.

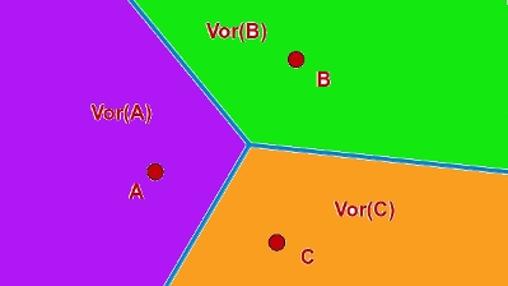
Lo cual es más fácil de entender si se observan las figuras.

El diagrama de Voronoi es una  forma matemática de dividir el mundo.Esta estructura que sirve para diferenciar el espacio en regiones puede aplicarse al fútbol, al diagnóstico de tumores o para evitar las colisiones de barcos en la costa. Dicen que es tan fácil que hasta un niño de tres años puede entenderlo.

Si está interesado en el tema puede consultar: https://www.abc.es/ciencia/abci-diagrama-voronoi-forma-matematica-dividir-mundo-201704241101_noticia.html.

Reflexionar para comprender lo que ve y lo que no se ve.